
[錯(cuò)因分析] 出錯(cuò)較多的是解答不夠嚴(yán)謹(jǐn), 例如計(jì)算出“當(dāng)0<a<2時(shí), 導(dǎo)數(shù)恒正”后, 就說(shuō)“f (x) 在R上為增函數(shù)”或“f (x) 在定義域?yàn)樵龊瘮?shù)”, 前者錯(cuò)在沒(méi)有考慮定義域, 后者錯(cuò)在沒(méi)有掌握好單調(diào)性判定定理, 忽視了本題里函數(shù)的定義域不是區(qū)間. 這些是實(shí)質(zhì)性的錯(cuò)誤. 還有類似的錯(cuò)誤, 如寫“f (x) 在(-∞, 1)∪(1, +∞)為增函數(shù)”, 這也可能僅僅是數(shù)學(xué)式寫錯(cuò)了, 不該用“∪”. 數(shù)學(xué)式寫錯(cuò)的還有“f (x) 在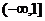 為增函數(shù)”, 這里不應(yīng)該用中括號(hào) “]”.
為增函數(shù)”, 這里不應(yīng)該用中括號(hào) “]”.
另一類錯(cuò)誤是第(Ⅰ)問(wèn)中不討論參數(shù)的值, 第(Ⅱ)問(wèn)中只討論a>0情形.
第(Ⅱ)問(wèn)中還有邏輯錯(cuò)誤. 例如“因?yàn)?i>f (0)=1, 故只要f (x) 在區(qū)間 (0, 1)為增函數(shù)”, 這樣也能得出正確結(jié)果, 但是推理過(guò)程是有錯(cuò)的, 錯(cuò)誤原因在于“f (0)=1, 且f (x) 在區(qū)間 (0, 1)為增函數(shù)”這個(gè)命題是“對(duì)任意 x∈(0,1) 恒有 f
(x) >
[復(fù)習(xí)提示] 近年總有含參數(shù)的函數(shù)(或數(shù)列)的考題, 一般都可用常規(guī)方法求解. 首先概念要清楚, 含參數(shù)的函數(shù)不是一個(gè)函數(shù), 參數(shù)的值不同, 就是不同的函數(shù). 其次, 應(yīng)該對(duì)參數(shù)分類, 即按照參數(shù)的不同變化范圍分成若干情形, 再分別討論.
文(22) (本小題滿分14分)
綜上可知, 所求 a的取值范圍為 a≤2.
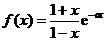 ≥
≥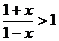 , 這時(shí)a滿足要求.
, 這時(shí)a滿足要求.
(?) 當(dāng)a>2時(shí), 由(Ⅰ) 知f (x) 在區(qū)間 (-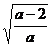 ,
,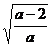 )為減函數(shù), 故在區(qū)間(0,
)為減函數(shù), 故在區(qū)間(0, 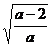 ) 內(nèi)任取一點(diǎn), 比如取
) 內(nèi)任取一點(diǎn), 比如取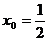
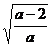 , 就有 x0∈(0, 1) 且 f (x0) < f (0) =1, 因而這時(shí)a不滿足要求.
, 就有 x0∈(0, 1) 且 f (x0) < f (0) =1, 因而這時(shí)a不滿足要求.
(?) 當(dāng)a≤0時(shí), 對(duì)于任意x∈(0, 1) 恒有
f (x) 在區(qū)間 (-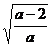 ,
,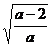 )為減函數(shù).
)為減函數(shù).
(Ⅱ) 參數(shù)a的變化范圍和(Ⅰ) 不同, 但由(Ⅰ) 知仍分三種情形討論.
(?) 當(dāng)0< a≤2時(shí), 由(Ⅰ) 知f (x) 在區(qū)間 (-∞, 1) 為增函數(shù), 故對(duì)于任意x∈(0, 1) 恒有 f (x) > f (0) =1, 因而這時(shí)a滿足要求.
f (x) 在區(qū)間 (-∞, -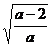 ), (
), (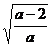 , 1), (1, +∞) 為增函數(shù),
, 1), (1, +∞) 為增函數(shù),
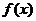
ㄊ
ㄋ
ㄊ
ㄊ
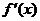
+
-
+
+
(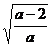 , 1)
, 1)
(1, +∞)
(-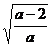 ,
,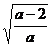 )
)
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com